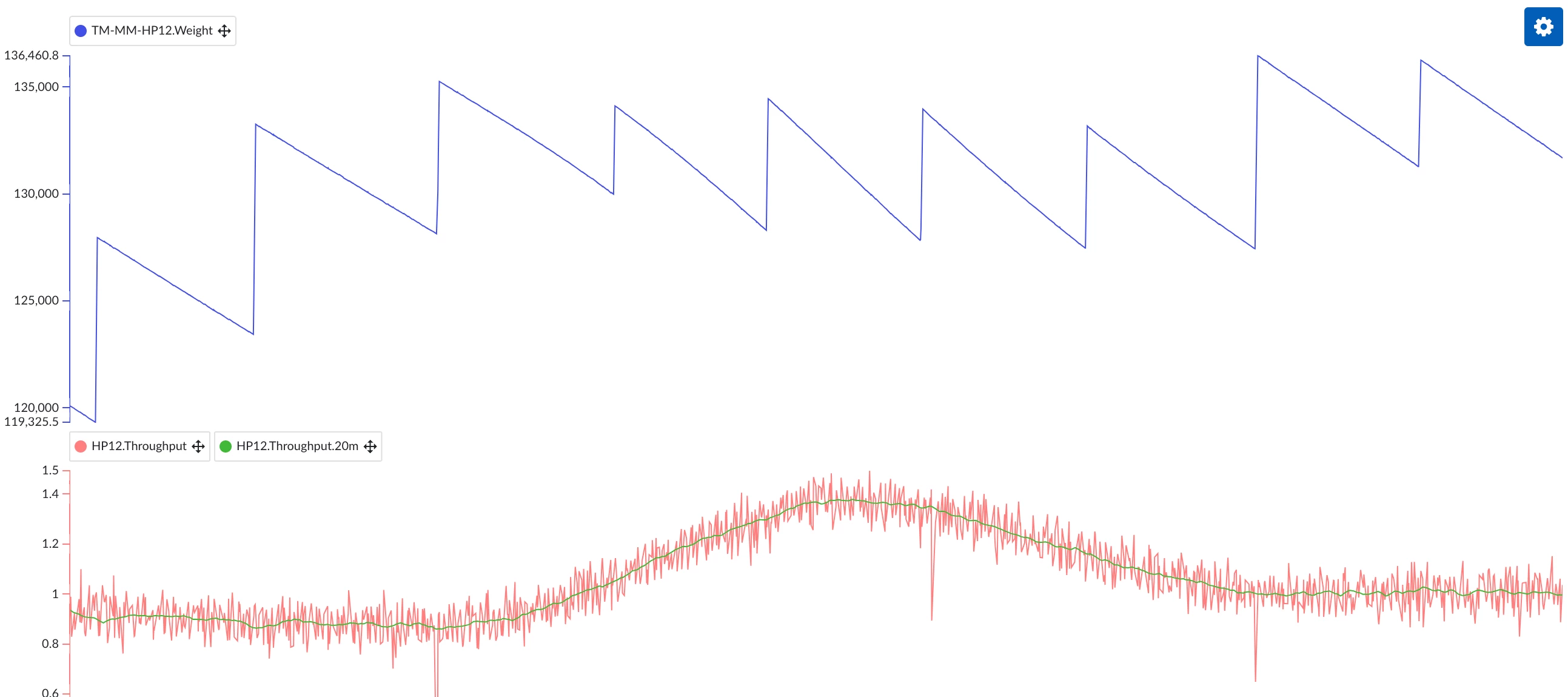
It can occur that we wish to know the flowrate of a certain material stream, but that the only measurement we have available is the weight or level of an intermediary vessel. This is especially applicable to the processing of solids, where measuring a flow directly is challenging. In this example, let's then work with the concept of deriving a mass flow from a total weight.

In essence, the mass flow is nothing more that then change (delta) of the weight of our vessel, multiplied by a constant value (to obtain the result in the desired units). As a starting point, we could for example take the weight in kg of our vessel 5 minutes ago, subtract the current weight, divided the result by 300 (the number of seconds in 5 minutes), to obtain a mass flow in kg/s:

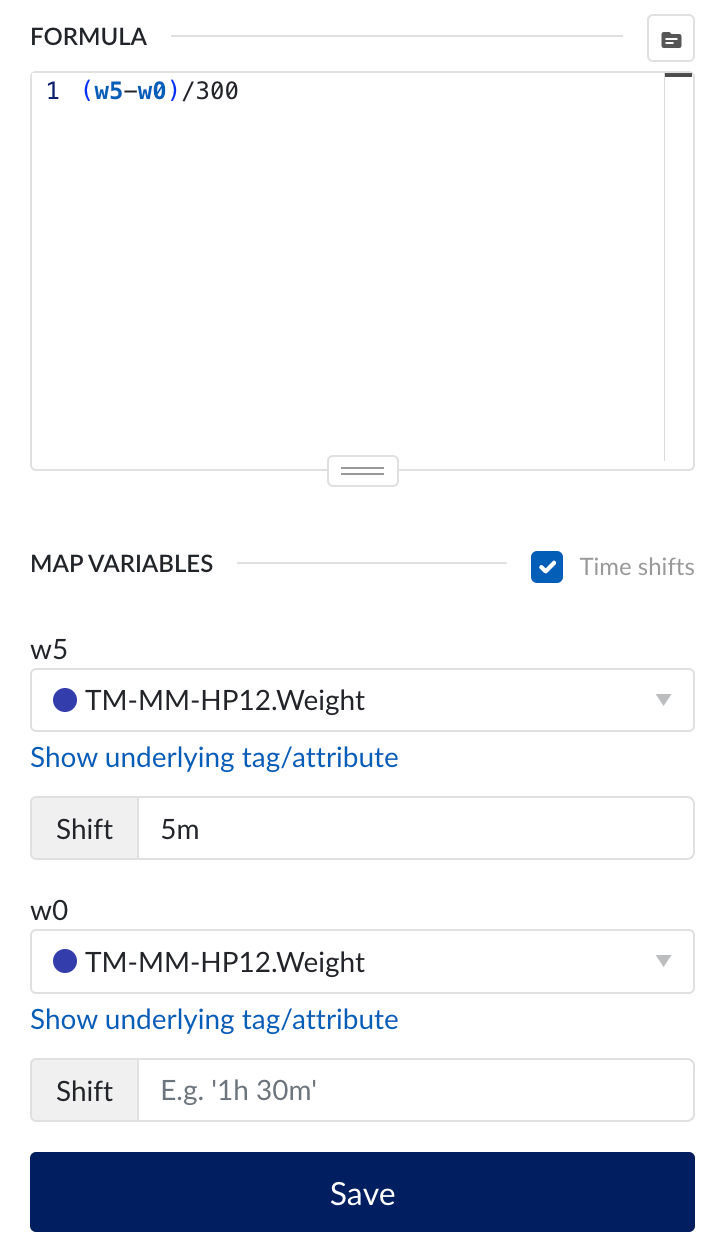
Note that the choice of the interval duration (here 5m) should depend on how noisy our weight measurement is. The longer we take the interval, the smoother our flow tag will become, at the cost of increasing the lag with which changes in flow are reflected in our formula tag. Some trial and error is in order here to find the minimal interval which creates a sufficiently smooth signal.

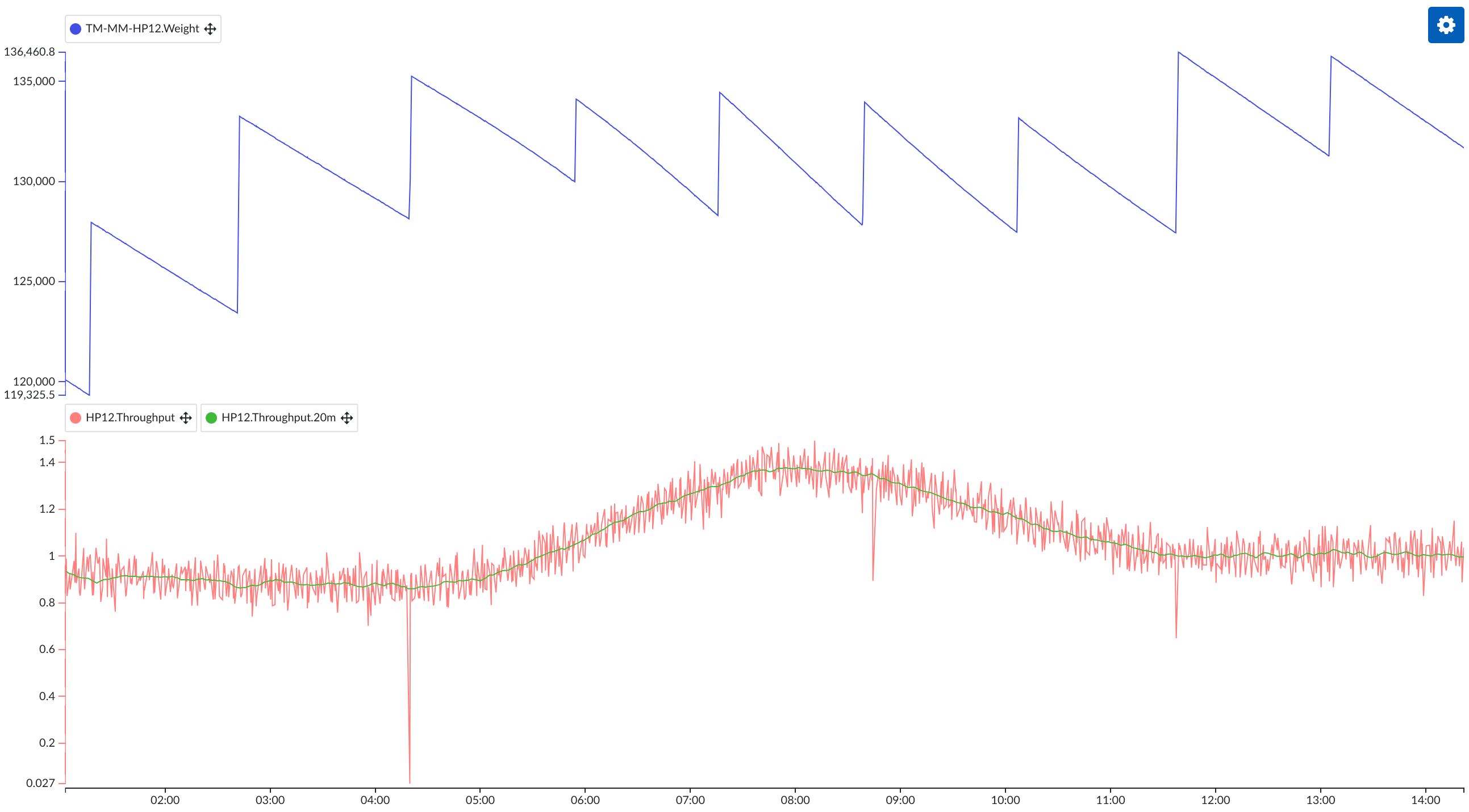
The real problem when creating a flow tag is of course that we also regularly fill our intermediary vessel, typically creating a sawtooth pattern where a continuous decrease is interrupted by sudden increases. In the naive formula implementation above, this will show as a huge negative flow rate. We will need to make our formula a bit more complex to account for this.

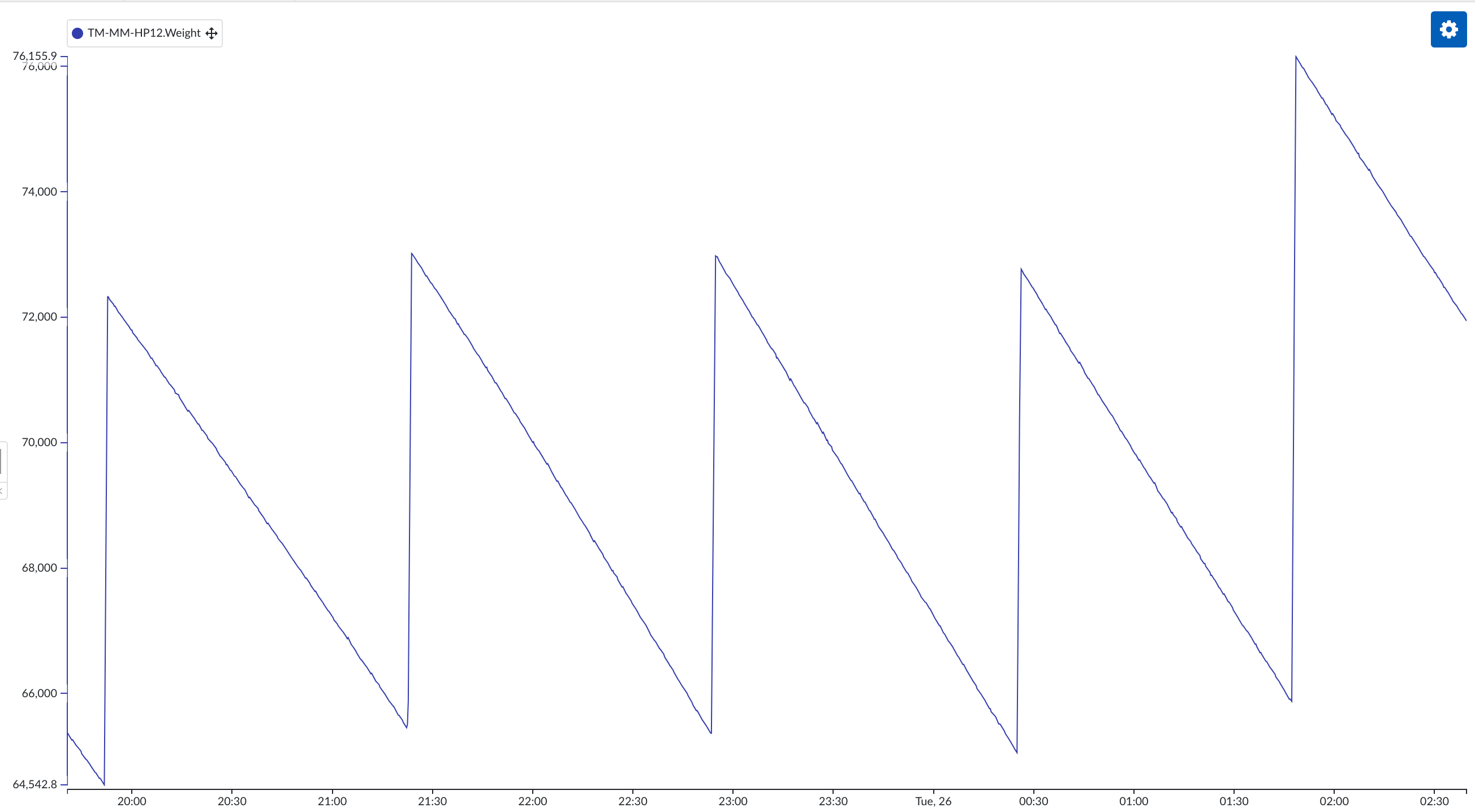
Filtering out these refills in a formula easy enough, as we can identify them by he apparent negative flow rate. The big question is what to do with these periods: if we measure only the weight, there is no way of knowing what the actual flow rate was during filling. We do want to provide some sort of best estimate, however, so that analytics we perform on our flow tag are more or less accurate. A typical use case would for example be integrating the flow tag to see how much material was processed in a certain timespan.

One approach to this issue that, in my experience, often produces the best results, is to assume that the flow rate during filling is equal to the flow rate just before refilling. In our formula, this means taking the flow rate of an amount of time ago that is certainly longer than the filling duration. In our example, filling always takes less than 7 minutes. So if we see that the current rate is negative, we can substitute the rate of 7 minutes ago (obtained by shifting our initial calculation by 7 minutes). In our formula, this will look like this:

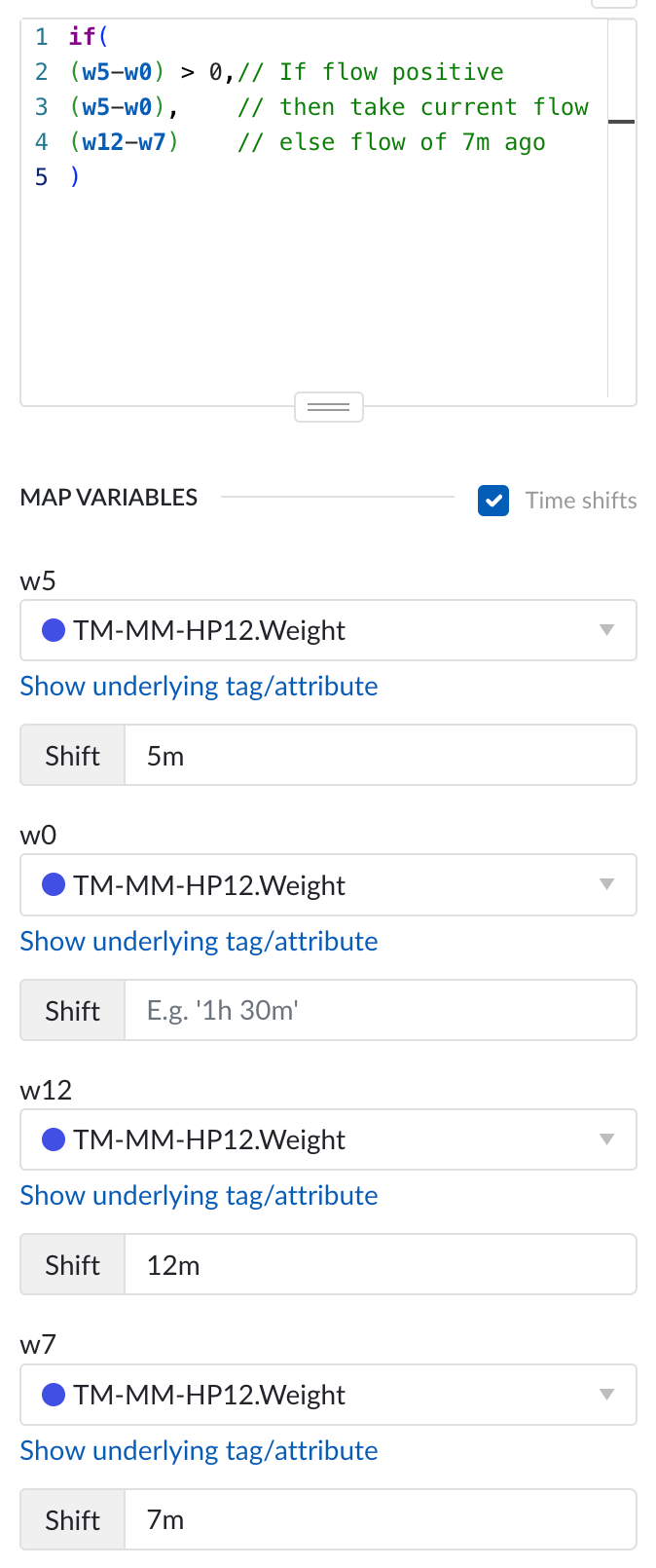
The resulting tag should do a decent job of ignoring the filling periods. Note that we can always go one step further and create an average aggregation of our formula to obtain an even smoother flow signal:

Hopefully, this small trick can help some of you get a more satisfactory calculation of flow rates!